Textklassifikation – Modelle trainieren und evaluieren
Im dritten und letzten Teil unserer Artikelreihe zur Textklassifikation geht es mit dem Training und der Evaluation von Modellen tief hinein ins Machine Learning: Das heißt, du wirst dabei sein, wenn wir anhand eines Beispieldatensatzes Modelle trainieren und evaluieren.
Nachdem wir im ersten Teil der Serie das Thema Textklassifikation mit einer kurzen allgemeinen Einführung kennengelernt haben und du im zweiten Teil einiges über den ersten Schritt der Textklassifikation – die Vorverarbeitung der Daten – gelernt hast, geht es in diesem dritten Teil ans eigentliche Machen. Wir hoffen, dich damit neugierig zu machen auf eine spannende Technik und dir falls du dich selbst an das Trainieren und Evaluieren von Machine-Learning-Modellen heranwagen möchtest, einen Vorgeschmack zu geben. Auf jeden Fall bekommst du ein paar Best Practices an die Hand, die es dir leichter machen können.
Die verwendeten Daten
Bevor wir mit dem Training loslegen können, brauchen wir natürlich Daten. Wer unsere Serie verfolgt hat, kennt ihn schon: unseren Datensatz Ten Thousand German News Articles Dataset. Dieser Datensatz enthält 10.273 Zeitschriftenartikel einer österreichischen Online-Zeitschrift, unterteilt in neun Kategorien. Das Ziel: Nach dem Training und der Evaluation soll unser Modell in der Lage sein, Artikel selbständig einer Kategorie zuzuordnen. Dafür wurden die Daten in Trainings- und Testdaten aufgeteilt. Wie viele Texte in jeder Kategorie vorhanden waren und wie groß der Anteil an Trainings- und Testdaten ist, zeigt Abbildung 1.
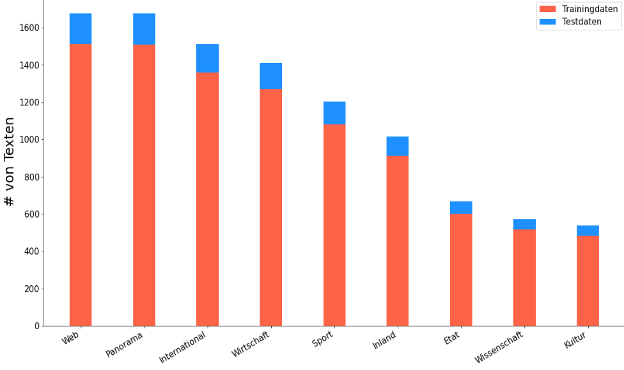 Abbildung 1: Anzahl an Texten per Artikelkategorie
Abbildung 1: Anzahl an Texten per Artikelkategorie
Genau betrachtet besteht der Prozess des Trainierens und Evaluierens von Modellen aus drei Einzelschritten: Feature Extraction, Modelle trainieren und Modelle evaluieren. Diese wollen wir uns im Detail ansehen:
Schritt 1: Feature Extraction und Baseline-Modelle
Beim Trainieren eines Machine-Learning-Modells füttern wir den Algorithmus bekanntlich mit Daten. Bei unserer österreichischen Online-Zeitschrift entspricht ein Zeitschriftenartikel einem Datensatz. Jeder Datensatz enthält also genau die Menge an Wörtern, die der Artikel beinhaltet.
Vielleicht erinnerst du dich an den Vorgang des Preprocessings aus dem zweiten Teil dieser Serie. Beim Preprocessing bringen wir den Datensatz in eine Form, die ein Machine-Learning-Algorithmus leicht verstehen kann. In eine einheitliche Form, die von Domäne und Ansatz unabhängig ist. Das können wir zum Beispiel durch das Konvertieren in Kleinbuchstaben und das Entfernen von Bindewörtern erreichen. Der nächste Schritt besteht darin, die Artikel in eine numerische Form bringen und sogenannte Features zu erstellen, die an das Modell weitergereicht werden. Ein Feature ist eine einzelne, messbare Einheit, die ein Element beschreibt. In unserem Beispiel sind Features also die Wörter, aus den der Artikel besteht, und somit beschreibt.
Wie stelle ich einen Text als Zahlen da?
Es gibt verschiedene Möglichkeiten, Textdaten als Zahlen zu repräsentieren. Wir haben uns für einen Bag-of-Words-Ansatz entschieden. Beim Bag-of-Words Ansatz wird nur das Auftreten von Wörtern betrachtet und nicht die Satzstruktur. Hier wäre also ein Feature und pro Artikel könnte für jedes Wort eine Zahl berechnet werden.
Auf diese Weise entsteht eine Dokument-Term Matrix, in der jede Zeile für einen Artikel und jede Spalte für ein Feature bzw. Wort aus diesem Artikel reserviert ist. In den Feldern der Matrix lässt sich seine Ausprägung als Zahlenwert ablesen. Der Zahlenwert Null würde aussagen, dass das Wort in diesem Artikel nicht vorkommt. Wie diese „Ausprägung” genau berechnet wird, hängt vom Verfahren ab.
| Fussball | Gewonnen | Mensch | Katze | ….. | |
| Artikel 1 | 1.2 | 0 | 1.6 | 0 | |
| Artikel 2 | 1.2 | 0 | 0 | 1.7 | |
| … |
Abbildung 2: Beispiel für eine Dokument-Term Matrix
Die Python-Bibliothek scikit-learn, die wir für die Implementierung benutzen, verfügt über zwei Varianten dieses Ansatzes:
- CountVectorizer(), bei dem nur die Häufigkeit jedes einzigartigen Wortes in einem Text betrachtet wird, und
- TfidfVectorizer(), bei dem zusätzlich noch mit einfließt, wie oft das Wort im kompletten Datensatz
Der TF-Teil des Begriffs steht für die Vorkommenshäufigkeit (Englisch: term frequency), und der IDF-Teil steht für die inverse Dokumenthäufigkeit (Englisch: inverse document frequency):
Gegeben Wort w und N Texte T0, …, TN-1
Anzahl von w in einem Text = count(w)
Anzahl aller Wörter im Text Ti ni
Anzahl an Texten, in denen w vorkommt count(ni(w))
TF(w) = count(w) / ni IDF(w) = log(N / count(ni(w)))
TF-IDF(w) = TF(w) x IDF(w)
Dabei nimmt der TF-IDF-Wert eines Wortes proportional zu, je häufiger das Wort im Text erscheint. Hingegen nimmt er ab, falls dasselbe Wort in vielen anderen Texten zu finden ist. Je geringer der Wert, umso weniger spezifisch wäre das Wort also für die Kategorie des Artikels. So hilft der TfidfVectorizer() dabei, zu entscheiden, welche Wörter aussagekräftig für eine Kategorie sind.
Für unser Vorhaben eine wichtige Eigenschaft! Deshalb nutzen wir diese Variante, um unsere Textdaten in eine sinnvolle numerische Repräsentation umzuwandeln.
Baseline-Modelle
Zunächst gilt: „je einfacher, desto besser”, also arbeiten wir mit einfachen, aber aussagekräftigen Baselines. Unter dem Begriff Baseline verstehen wir eine erste, möglichst einfache Lösung, an der wir die Machbarkeit des Problems überprüfen können und die uns hilft, das Machine-Learning-Problem besser zu verstehen. Auf dieser Basis können wir später komplexer werden und die Performance immer weiter verbessern.
In unserem Fall verwenden wir Standardmodelle, von denen wir wissen, dass sie in den meisten Fällen gute Ergebnisse liefern. Für die Textklassifikation eignen sich beispielsweise das Naive-Bayes-Modell und die Support Vector Machine. Konkret entscheiden wir uns für drei Modelle: zwei Naive-Bayes-Modelle – Multinomial-Naive-Bayes-Klassifikator und Complement-Naive-Bayes-Klassifikator – und einen Support-Vector-Machine.
Damit du dir unter den drei Modellen etwas vorstellen kannst, beschreiben wir kurz den mathematischen Hintergrund und schauen uns jeweils ein kleines Beispiel aus unserem Datensatz an. Wir benutzen hier nur vier Klassen aus den neun. (Siehe Abbildung 3)
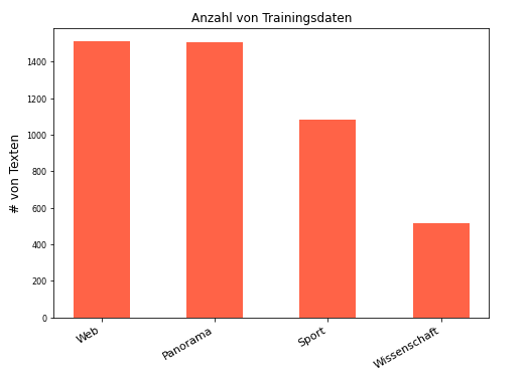 Abbildung 3: Anzahl von Trainingsdaten nach Klasse
Abbildung 3: Anzahl von Trainingsdaten nach Klasse
Multinomial-Naive-Bayes-Klassifikator
Der Multinomial-Naive-Bayes-Klassifikator basiert auf einem der wichtigsten Sätze der Wahrscheinlichkeitsrechnung – dem Satz von Bayes – und wird für Klassifikationsaufgaben wie die Textklassifikation benutzt. Features sind hier numerische Werte, die Anzahl der Wörter im Text oder wie in unserem Fall TF-IDF-Werte.
Während des Trainings lernt das Modell bestimmte spezifische Merkmale einer Kategorie kennen und nutzt diese Erkenntnisse später bei der Klassifikation. Nach dem Prinzip „Je mehr Features einer Klasse im Text enthalten sind, desto größer ist die Wahrscheinlichkeit, dass der Text zu der entsprechenden Klasse gehört” wird die Klasse mit der größten Wahrscheinlichkeit ausgewählt.
Nehmen wir an, während des Trainings hat unser Modell gelernt, dass Texte, die zur Kategorie Web gehören, bestimmte Wörter in größere Anzahl enthalten wie Internet, online, anschauen, empfangen”. In Texten der Kategorie Sport kommen hingegen häufiger Wörter vor wie „ Motorsport, Spiel u. s. w.
Ein Beispiel:
Sky Q kann auch rein über Internet genutzt werden. Ihr könnt Formula 1 und alle euren Lieblingsinhalte zum Thema Motorsport auch online im Internet empfangen.
Dieser Artikel enthält vier Wörter der Kategorie Web (2x Internet, 1x online, 1x empfangen) aber nur ein Wort der Kategorie Sport (1x Motorsport). Also ist die Wahrscheinlichkeit größer, dass der Text zur Kategorie Web als zur Kategorie Sport gehört.
Complement-Naive-Bayes-Klassifikator
Der Complement-Naive-Bayes-Klassifikator ist eine Variante des Multinomial-Naive-Bayes-Klassifikators, die sich für nicht balancierte/unausgeglichene Daten eignet. Damit lässt sich beispielsweise aus dem Balkendiagramm der Abbildung 3 herauslesen, dass deutlich mehr Texte in den Kategorien Web und Panorama veröffentlicht wurden als in den Kategorien Sport und Wissenschaft.
Bei diesem Klassifikator berechnen wir für jede Klasse die Wahrscheinlichkeit, dass ein Text nicht zu dieser Klasse gehört. Folglich wird der kleinste Wert ausgewählt, da es am unwahrscheinlichsten ist, dass der Text nicht zu der Kategorie gehört, und somit am ehesten dazugehört.
Der Complement-Naive-Bayes-Klassifikator erzielt bei der Textklassifikation übrigens regelmäßig eine bessere Performance als der Multinomial-Naive-Bayes-Klassifikator.
Für weitere technische Details lohnt es sich, einen Blick in ein Paper der Autorengruppe um Jason Rennie und Lawrence Shih zu werfen, die das Modell entwickelt hat: „Tackling the poor assumptions of naive bayes text classifiers„ in: Proceedings of the Twentieth International Conference on Machine Learning (ICML-2003), Washington DC, 2003 (Link: https://people.csail.mit.edu/jrennie/papers/icml03-nb.pdf)
Support-Vector-Machine
Support-Vector-Machines können sowohl in Klassifikationsaufgaben als auch zur Regressionsanalyse benutzt werden. Sie können Daten mit sehr vielen Features – wie es bei einer Textklassifikation der Fall ist – effektiv in verschiedene Klassen teilen. Dazu braucht das Modell nicht viel Speicherplatz und erzielt auch auf einer kleinen Datenbasis gute Ergebnisse.
Ein Linear-Support-Vector-Klassifikator kann Daten in zwei oder mehr Kategorien unterteilen. Wie eine solche Aufteilung aussehen kann, zeigt Abbildung 4. Mithilfe von farbigen Punkten teilt das Modell die Texte in die vier Kategorien aus unserem Beispieldatensatz.
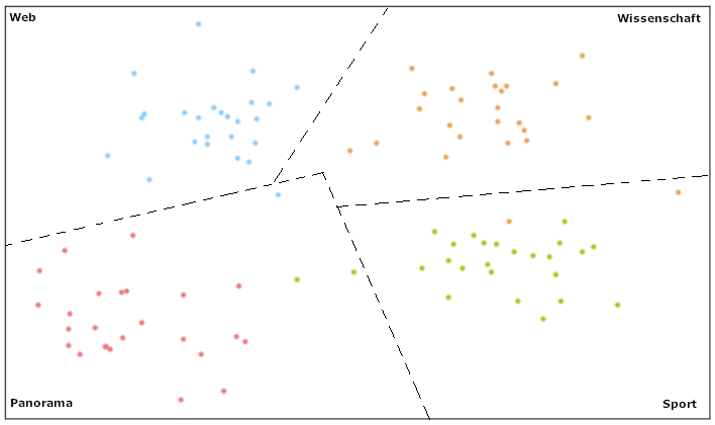
Abbildung 4: Support-Vector-Machine-Modell für vier Klassen
Schritt 2: Modelle trainieren
Nachdem wir unserer Daten vorbereitet und unsere Modelle ausgesucht haben, kann das Training beginnen.
Was bedeutet es eigentlich, ein Modell zu trainieren? Was genau steckt hinter dem Vorgang, den wir „Training“ nennen?
Hinter jedem Modell verbirgt sich ein Algorithmus. Trainieren wir das Modells, so erhält der Algorithmus die vorbereiteten numerischen Daten mit der Kategorie zu jedem einzelnen Sample und versucht, die Beziehung zwischen einem Beitrag und seiner Kategorie zu verstehen und zu lernen.
Trainingsdaten und Testdaten
Damit wir unsere Modelle später valide evaluieren können, unterteilen wir unsere Daten in zwei Gruppen: Trainingsdaten und Testdaten:
- Trainingsdaten benutzen wir beim eigentlichen Training unserer Modelle – das sind die Daten, aus denen das Modell die Zusammenhänge zwischen der Kategorie und dem Beitrag lernt.
- Testdaten nutzen wir, um unser Modell zu evaluieren. Wie bei einer Klassenarbeit muss das Modell mit ihm unbekannten Daten arbeiten. Hier erfahren wir, wie präzise es das Gelernte auf neue Artikel anwenden kann. Ist dies der Fall, so wird das Modell später auch bei Echtdaten eine gute Performance abliefern.
Schritt 3: Modelle evaluieren
Beim letzten Schritt geht es darum, die Performance unserer Modelle zu testen. Dafür hatten wir ja einen Testdatensatz vorbereitet. Mit Texten dieses Datensatzes füttern wir das Modell, bis es uns eine Kategorie zu jedem Text auswirft. Die Ergebnisse vergleichen wir anschließend mit den echten Kategorien der Texte.
Am Ende beweist eine Konfusionsmatrix, wie gut die Prognosequalität unseres Algorithmus war. Wie das in unserem Beispiel bei Artikeln in der Kategorie Sport aussieht, zeigt Abbildung 5.
| Artikel ist Sportartikel | Artikel ist kein Sportartikel | |
| Modell hat Artikel als Sport erkannt | Richtig positiv – Modell hat Artikel richtig erkannt | Richtig negativ – Modell hat erkannt das es sich nicht um Sport handelt |
| Modell hat Artikel als nicht Sport bewertet | Falsch negativ – Modell dachte der Artikel gehört fälschlicherweise zu Sport | Falsch positiv – Modell hat nicht erkannt das der Artikel zu Sport gehört |
Abbildung 5: Beispiel für eine Konfusionsmatrix
Wie nutzten wir die Konfusionmatrix?
Es gibt drei Metriken, die zur Evaluierung von Klassifikationsmodellen benutzt werden: Accuracy, Precision und Recall.
- Die Accuracy berechnen wir, indem wir die Anzahl an richtigen Ergebnissen, also richtig positiv und richtig negativ, durch die Anzahl aller Ergebnisse teilen.-> (richtig positiv + richtig negativ) / alle Ergebnisse
- Die Precision wird berechnet als Anteil der relevanten Beispiele (z.B. die richtig positiven) an allen Ergebnissen, die als Mitglieder einer bestimmten Klasse, klassifiziert sind.-> richtig positiv / (richtig positiv + falsch positiv)
- Der Recall ist der Anteil an Beispielen, die zu einer Klasse klassifiziert werden, geteilt durch alle Beispiele, die in der Tat zu der Klasse gehören.-> richtig positiv / (richtig positiv + richtig negativ)
Umsetzung in Python
Im Folgenden zeigen wir, wie wir die Schritte aus der Theorie in unserem Projekt umgesetzt haben und welche Ergebnisse dabei herausgekommen sind.
Für die Umsetzung haben wir in Python die folgenden Bibliotheken benutzt: pathlib, pandas und sklearn.
import pandas as pd import pathlib from pathlib import Path from sklearn import metrics |
Aufteilung in Test- und Trainingsdaten
Zuallererst – noch bevor die Daten an das Modell übergeben werden können, unterteilen wir die Gesamtmenge in Trainingsdaten und Testdaten. Unser Datensatz hatte dafür schon zwei Dateien vorgesehen.
Dieses Code-Beispiel zeigt, wie wir mit Hilfe der Bibliothek pathlib auf diese beiden Datenmengen zugreifen:
# Paths to the csv files
training_set = Path("data/train/training_preprocessed.csv")
test_set = Path("data/test/test_preprocessed.csv")
|
Einlesen der Daten
Mit Hilfe der Bibliothek pandas lesen wir die Daten aus den CSV-Dateien aus und teilen diese auf nach Inhalte (die Wörter des Artikels) und deren Kategorien (z. B. Sport
Mit den Features füttern wir das Modell. Die Kategorien bezeichnen das gewünschte Ergebnis.
# read and display as data frame df_train = pd.read_csv(training_set_preprocessed, encoding='utf-8', error_bad_lines=False) # split into text -> (x), and category (=label) -> (y) x_train, y_train = df_train['text'], df_train['category'] |
Feature Extraction
Bei der Feature Extraction werden die Daten in eine numerische Form gebracht, also in Zahlen umgerechnet. Wenn du dich an die Theorie dahinter nicht mehr so genau erinnerst, dann wirf noch einmal schnell einen Blick auf Schritt 1: Feature Extraction.
Mit der Bibliothek sklearn können wir den TF-IDF-Ansatz ganz einfach implementieren:
from sklearn.feature_extraction.text import TfidfVectorizer, CountVectorizer, TfidfTransformer count_vect = CountVectorizer() x_train_counts = count_vect.fit_transform(x_train) x_train_tfidf = TfidfTransformer().fit_transform(x_train_counts) |
Jetzt sind die Daten bereit für die Trainingsphase und haben folgende Dimensionen:
'Train: ((8620, 164288), (8620))'
Für uns bedeutet das wir haben 8.620 Artikel mit je 164.288 Features.
Trainieren der Modelle
Nun können wir die Modelle aus sklearn importieren. Wie geplant werden wir zwei Bayes-Modelle – Multinomial-Naive-Bayes und Complement-Naive-Bayes – und eine Support Vector Machine trainieren:
from sklearn.naive_bayes import MultinomialNB from sklearn.naive_bayes import ComplementNB from sklearn.svm import LinearSVC |
Das eigentliche Training wurde von der Bibliothek schon implementiert, sodass wir den Trainingsprozess direkt starten können. Dafür wenden wir die .fit()-Funktion jedes Modells auf die Daten an:
naive_bayes = MultinomialNB().fit(x_train_tfidf, y_train) complement_nb = ComplementNB().fit(x_train_tfidf, y_train) linear_svc_model = LinearSVC().fit(x_train_tfidf, y_train) |
Ergebnisse
Für die Artikel unserer österreichischen Online-Zeitung kann ein Artikel in einer von neun Kategorien eingeordnet werden. Die Konfusionsmatrix zeigt, welche der Kategorien jeweils vom Multinomial Naive Bayes Modell klassifiziert wurden.
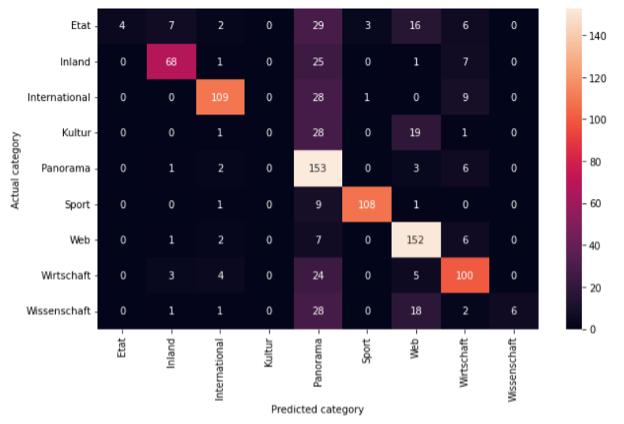
Abbildung 6: Konfusionsmatrix für das trainierte Multinomial-Naive-Bayes-Modell.
Abbildung 6 zeigt die Konfusionsmatrix des Multinomial-Naive-Bayes-Modells. Daraus wird ersichtlich, dass z. B Sportartikel sehr gut erkannt werden. Von 112 Testartikeln wurden 108 korrekt klassifiziert. Im Vergleich wurden bei Artikeln der Kategorie Panorama von 331 Artikeln nur 153 korrekt klassifiziert.
Daraus ergibt sich die folgende Genauigkeit (Accuracy) pro Kategorie:
Etat: 0.059
Inland: 0.66
International: 0.74
Kultur: 0.0
Panorama: 0.92
Sport: 0.9
Web: 0.9
Wirtschaft: 0.73
Wissenschaft: 0.10
Außerdem können wir auch die generelle Genauigkeit für das ganze Modell berechnen. Dafür nutzen wir die Scikit Funktion accuracy_score, die sich auf die Artikel des Testdatensatzes bezieht, die richtig zugeordnet wurden.
sklearn.metrics.accuracy_score(y_true, y_pred, *, normalize=True, sample_weight=None)
Bei unserem Multinomial Naive Bayes Modell liegt dieser Wert bei 69.38 %.
Dieses Verfahren haben wir für alle Modelle durchgeführt. Der Support Vector Machine liefert die besten Ergebnisse mit einer Gesamtgenauigkeit von 83.35 % und entsprechend hohen Genauigkeitswerten in jeder Kategorie:
Etat: 0.64 Inland: 0.80 International: 0.76 Kultur: 0.85 Panorama: 0.82 Sport: 0.97 Web: 0.84 Wirtschaft: 0.86 Wissenschaft: 0.89
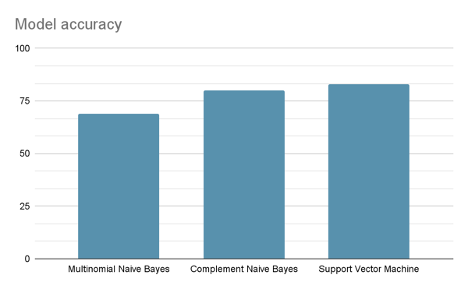
Abbildung 7: Vergleich der Genauigkeit der Modelle anhand von dem Testdatensatz
Wie könnte es weitergehen? … ein Blick in die Zukunft
Vielleicht fragst du dich, wie es jetzt in unserem Beispiel weitergeht. Es gibt verschiedene weiterführende Themen, die als nächste Schritte interessant wären. Die Machine-Learning-Modelle könnten zum Beispiel mithilfe des Parameter-Tunings noch weiter optimiert werden. Auch das große Thema neuronale Netzwerke haben wir außen vorgelassen. Diese erzielen oft bessere Ergebnisse, sind jedoch schwieriger nachzuvollziehen.
Autoren: Luca Pomer, Galina Angelova und Conrad Dollinger
Alle Teile dieser Serie:
Teil 1: Textklassifikation – eine Einführung
Teil 2: Textklassifikation – Vorverarbeitung der Daten
Teil 3: Textklassifikation – Modelle trainieren und evaluieren




