Aufbau von Blockchiffren:
Blockchiffren verschlüsseln blöckeweise, d.h. sie teilen den zu verschlüsselnen Text in Blöcke auf, die sie dann einzeln verschlüsseln. Blockchiffren haben zwei grundlegende Operationen, Konfusion und Diffusion.
Die Konfusion soll den Text konfus, also unleserlich und für den Menschen unverständlich machen.
Die Diffusion soll einzelne Änderungen am Schlüssel auf das ganze Ergebnis der Verschlüsselung (=verschlüsselter Text) auswirken.
Wichtig für ein gutes Verständnis von Verschüsselungsmethoden sind die verschiedenen Zahlensysteme wie das Binär -und das Hexadezimalsystem. Des Weiteren wird häufig auf die modulare Reduktion zurückgegriffen, die ebenfalls wichtig für ein gutes Verständnis ist, da so die Zahlen klein bleiben, dass auch jedes Gerät in der Lage bleibt sicher zu verschlüsseln, auch wenn die Zahlen dabei recht groß werden können.
Am Ende der Seite befinden sich Links, falls diese noch nicht klar sind.
Runden von AES:
AES ist iterativ, d.h. er wiederholt Abschnitte seiner Funktionsweise, diese Abschnitte heißen Runden. Je nach gewählter Schlüssellänge variieren diese Runden zwischen 10, 12 und 14.
Key-Addition-Schicht:
Die Key-Addition-Schicht „xoriert“ den jeweiligen Unterschlüssel aus dem hier nicht betrachteten Schlüsselfahrplan, auf die Blocklänge. Da bei der XOR-Operation die zu „xorienden“ Zahlen gleich viele Binärziffern benötigen, beträgt der Unterschlüssel unabhängig von der zu Beginn ausgewählten Schlüssellänge, die 128, 192 und 256 Bits betragen kann, 128 Bit, da dies die fixe Blocklänge ist.
Byte-Substitution-Schicht:
Zu Anfang werden die 128 Bit Blocklänge in 16 ein Byte große Blöcke aufgeteilt.
Wenn man einen einzelnen Block betrachtet, besteht dieser aus zwei Hexadezimalziffern, mit diesen kann man einen Tabelleneintrag in der S-Box des AES ermitteln (1. Stelle gibt Zeile an und 2. Stelle gibt Spalte an).
Shift-Rows-Schicht:
Für die zweite Schicht werden die 16 Blöcke in eine 4×4 Matrix eingetragen, wobei die Einträge nicht von links nach rechts, sondern von oben nach unten eingetragen werden.
Dann werden die Reihen wie gezeigt verschoben:


Wie man an dem Beispiel erkennen kann, sorgt die Verschiebung dafür, dass man das anfangs noch zu lesende Wort Verschluesselung nun nicht mehr lesen kann, da an dieser Stelle nun VHSGCSNSEURULELE steht.
Mix-Column-Schicht:
Für die Mix-Column-Schicht werden die Bytes in Polynome umgewandelt. Hierfür werden die Bytes in achtstellige Binärzahlen aufgeschrieben und dann von rechts nach links mit aufsteigendem Exponenten in ein Polynom umgewandelt.
Bsp.:
1000 1000 = 0 * x^0 + 0 * x^1 + 0 * x^2 + 1 * x^3 + 0 * x^4 + 0 * x^5 + 0 * x^6 + 1 * x^7 = x^3 + x^7

Dann werden alle Bytes in vier Vektoren eingeteilt, diese entsprechen den Spalten der 4×4 Matrix nach der Shift-Rows-Schicht. Diese vier Vektoren werden nacheinander mit der rechtsstehenden festgelegten Matrix via Matrix-Vektor-Multiplikation als Polynom verrechnet.
Um auch hier zu verhindern, dass die Polynome zu groß werden und so den Wert eines Bytes überschreiten würden, wird auch hier reduziert. Dies erfolgt durch ein Reduktionspolynom, welches bei AES auf P(x)= x^8 + x^4 + x^3 + x + 1.
Durch Umstellung und wegen der Binärdarstellung der ursprünglichen Zahl, aus welcher das Polynom abgeleitet wurde, kann man P(x) so umstellen, dass dort folgende Gleichung steht:
x^8 = x^4 + x^3 + x + 1
Um die gelösten Polynome wieder in Hexadezimalzahlen umzuwandeln, wird wie zu Beginn der Umweg über die Binärzahlen genommen und kann äquivalent zurückgerechnet werden.
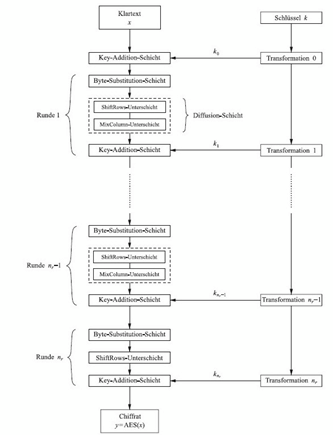
Um mit AES zu verschlüsseln, muss man diese Schichten einer einzelnen Runde immer durchführen außer in der letzten Runde, dort wird die Mix-Column-Schicht übersprungen.
Des Weiteren wird aus historischen Gründen vor der ersten Runde der ersten Rundenschlüssel „xoriert“, also die Key-Addition-Schicht durchgeführt, dies hat keine großen Auswirkungen auf die Sicherheit von AES.




